The wireframe on the left is an inside out view of the mesh that define the scene. On the right is the final rendered image using ray-tracing techniques. Image Credits: Science behind Pixar

Pixar characters like the dependable Woody, endearing Dory, or bold Merida from Brave come to life through a blend of creativity and mathematics. Designers and artists think in terms of images and shapes, envisioning characters and worlds, while computers operate on equations and numerical data. To bridge these two worlds, designers rely on coordinate geometry. This concept allows them to precisely define the positions and movements of digital objects within a virtual space. Geometry, a fundamental branch of mathematics dealing with points, lines, surfaces, and solids, forms the backbone of computer graphics and animation. It plays a critical role in defining the shapes, structures, and movements of digital objects, whether for video games, movies, or virtual reality. By leveraging geometric principles and algorithms, animators and graphic designers can craft realistic and visually stunning images. These algorithms model everything from the curves of characters to intricate environments, and simulate phenomena like light and shadows. This precise framework enables artists to translate their creative visions into detailed and believable 3D animations, captivating audiences with immersive digital worlds.

In this post, we'll look at some of the scientific principles behind the creation of these digital masterpieces. We will examine modeling, which defines the structure of characters and environments; lighting, which simulates realistic illumination and shading; materials, which add texture and physical properties; and rendering, which synthesizes these elements into the final, high-quality image. Lets see how computer graphics exists at the intersection of art and mathematics, with the goal of realism in animation.

• Modeling: the art of creating 3D worlds Modeling is the foundation of computer graphics, where geometry transforms imagination into digital reality. By understanding geometric principles, animators can build intricate models that serve as the blueprint for their creations. Here we provide a brief overview of some of the key aspects of modeling.

• Surface modeling: sculpting in digital space Surface modeling involves creating 3D objects via an outer shell. This process uses geometric shapes such as polygons and NURBS (Non-Uniform Rational B-Splines) to represent the complex surfaces. By manipulating these shapes, animators can sculpt detailed and lifelike characters, vehicles, and landscapes, defining their contours and textures. Polygons are the simplest building blocks, forming flat surfaces that can be combined to approximate complex shapes. NURBS, on the other hand, offer smooth and precise curves, ideal for organic forms like faces and clothing.

• Mesh Modeling: building the skeleton Mesh modeling focuses on constructing a network of vertices, edges, and faces to form the skeleton of a 3D model. This wireframe structure is essential for defining the shape and volume of objects. Geometric transformations like translation, rotation, and scaling are applied to these meshes to refine the model's form, enabling the creation of detailed and realistic digital representations. Vertices represent points in space, edges connect these points to form lines, and faces are the surfaces enclosed by edges. Together they create a flexible framework that can be manipulated to achieve the desired shape.

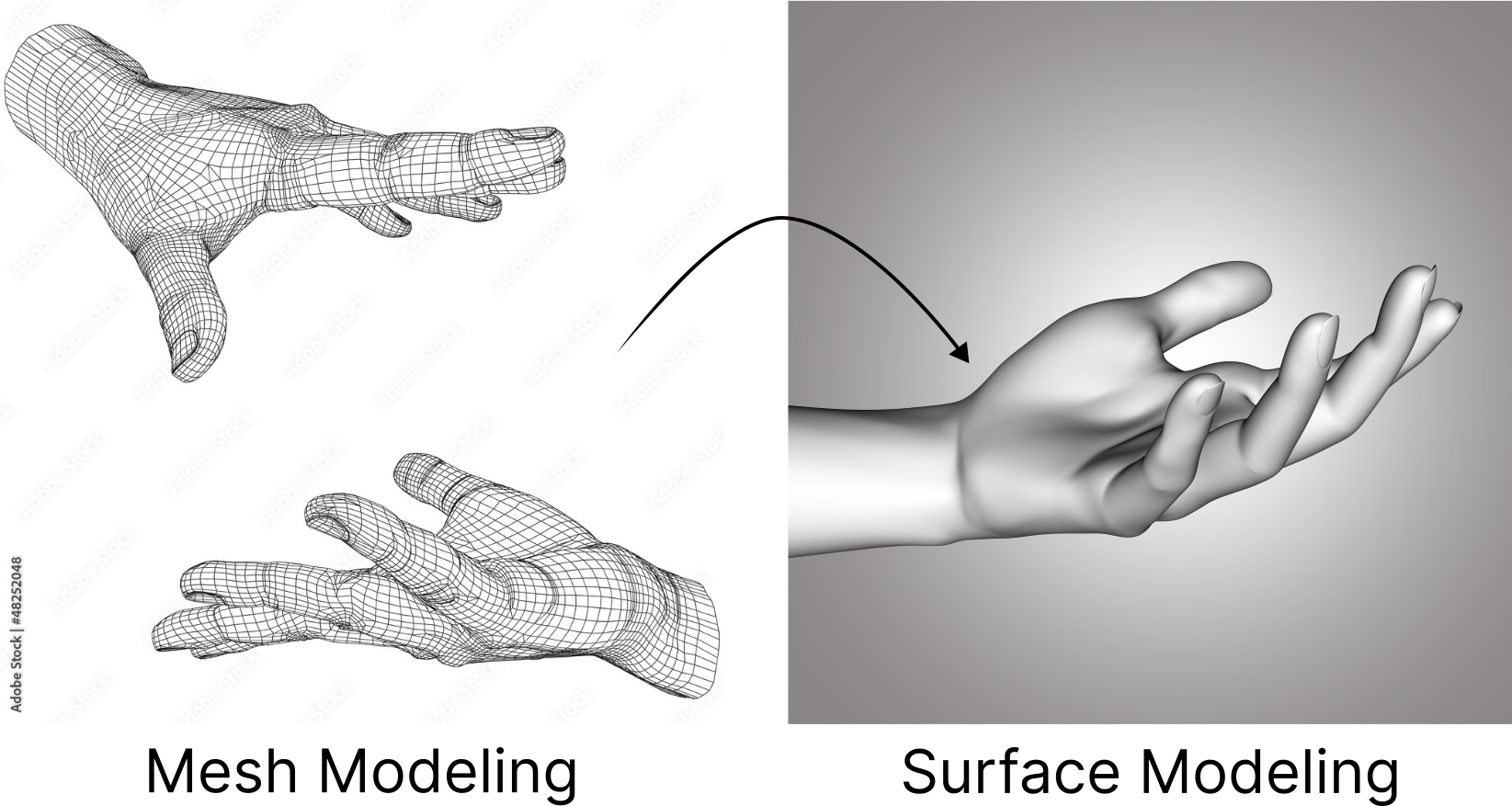Left: A wireframe mesh model illustrating the vertex, edge, and face structure of a human hand. Right: An example of surface modeling showing the creation of a human hand.

Materials: Bringing Surfaces to Life

Materials play a crucial role in defining the appearance and physical properties of 3D surfaces. Geometry is fundamental in determining how these materials interact with light, enhancing the realism of digital objects. Let us now look at properties such as textures, shaders, reflectance that define the behaviour of materials.

• Texturing and Mapping: Texturing involves applying images or patterns to the surface of 3D models. UV mapping, a geometric technique, is used to unwrap the model's surface onto a 2D plane, ensuring textures are accurately placed. This process helps in creating realistic skin, fabrics, and other surface details. By projecting a 2D image onto the 3D surface, artists can add intricate details without having to model every small feature. This technique ensures that the textures align perfectly with the geometry of the model, adding depth and realism.

• Shaders and Reflectance: Shaders are algorithms that determine how light interacts with surfaces. By using geometric properties like surface normals and tangent spaces, shaders can simulate various material characteristics, such as glossiness, transparency, and subsurface scattering, bringing surfaces to life with stunning realism. Surface normals are vectors that point perpendicular to the surface, helping to calculate how light bounces off. Tangent spaces provide a local coordinate system to apply effects like bump mapping, which simulates small surface details. Subsurface scattering mimics the way light penetrates translucent materials, creating lifelike skin and other organic materials.

The importance of materials and lighting in 3D rendering. The image shows rough cubes and a glossy ball, highlighting how different materials behave under the same lighting conditions. The cubes are assigned a diffuse BSDF(Bilateral Scattering Diffusion Function) material, while the ball uses a glossy BSDF material. The scene is lit with a sun lamp at a strength of 4.5 units, creating realistic shadows and reflections.

Light & Camera: Capturing the Perfect Shot

Geometry plays a pivotal role in simulating light behavior and camera dynamics, essential for creating believable scenes in animation.

• Light: the essence of realism: Understanding geometric principles of light propagation and reflection is crucial for simulating realistic illumination. Techniques like ray tracing and global illumination rely on geometry to calculate how light interacts with objects, producing shadows, highlights, and realistic reflections. Ray tracing follows the path of light rays as they bounce around a scene, calculating reflections, refractions, and shadows to create highly realistic images. Global illumination goes a step further, simulating the way light bounces off surfaces and affects the entire scene, creating natural and immersive lighting.

• Camera: the digital lens: In virtual environments, cameras operate based on geometric principles of perspective and depth. Proper camera placement and movement, guided by geometric algorithms, ensure accurate representation of scenes, enhancing the narrative and visual impact of the animation. Perspective projection creates the illusion of depth by making distant objects appear smaller, just like in real life. Depth of field adds a level of realism by simulating the way cameras focus on a particular plane, blurring objects that are closer or farther from the focal point.

• Rendering: from 3D models to 2D images: Rendering converts 3D models into 2D images, the process of projection in a loose sense which is deeply rooted in geometry. Accurate rendering ensures the final output is visually compelling and realistic.

  Kajiya rendering equation: The Kajiya rendering equation is a fundamental concept in rendering, describing how light is transferred around a scene. By solving this equation, animators can achieve global illumination effects, accurately simulating how light bounces and interacts with surfaces. This equation takes into account both direct light from sources and indirect light reflecting off surfaces, creating a comprehensive and realistic lighting model. This equation for light radiance is given by:

  $L_o(x, \omega_o) = L_e(x, \omega_o) + \int_{\Omega} f_r(x, \omega_i, \omega_o) L_i(x, \omega_i) (\omega_i \cdot n) \, \text{d} \omega_i$.

  The variables in the above equations are defined as:

  • $L_o(x, \omega_o)$: Outgoing light radiance at point $x$ in direction $\omega_o$

  • $L_e(x, \omega_o)$: Emitted light radiance at point $x$ in direction $\omega_o$

  • $f_r(x, \omega_i, \omega_o)$: Bidirectional Reflectance Distribution Function (BRDF) at point $x$, incoming direction $\omega_i$, and outgoing direction $\omega_o$

  • $L_i(x, \omega_i)$: Incoming light radiance at point $x$ from direction $\omega_i$

  • $\omega_i \cdot n$: Cosine of the angle between the incoming light direction $\omega_i$ and the surface normal $n$

  • $\int_{\Omega} \, \text{d} \omega_i$: Integral over the hemisphere of all incoming light directions $\omega_i$

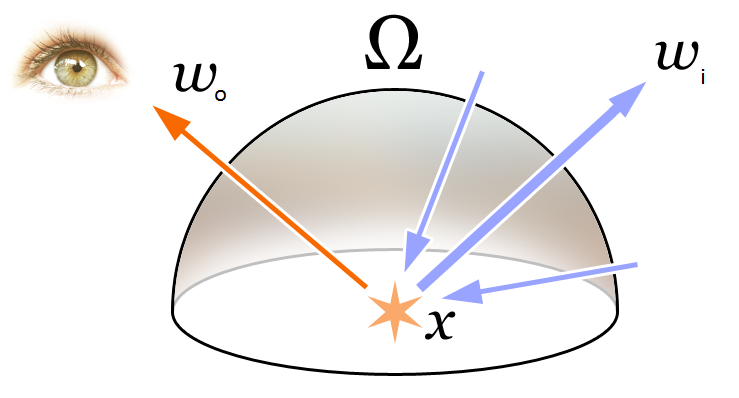
Visualization of different elements in the Kajiya rendering equation. The rendering equation describes the total amount of light emitted from a point $x$ along a particular viewing direction, given a function for incoming light. $w_i$ is the direction of incoming light and $w_o$ is the direction of outgoing light at $x$, $\Omega$ is the hemispherical domain around which all light is integrated. Image Credits: By Timrb - Own work, CC BY-SA 3.0.

The rendering equation is used to compute the global illumination in a scene, taking into account how light interacts with surfaces through reflection, refraction, and scattering. It provides a comprehensive framework for simulating realistic lighting in computer graphics, enabling the creation of visually stunning and believable images.

• Geometric transformations in rendering: During rendering, geometric transformations like projection and clipping are applied to convert 3D coordinates into 2D screen space. These transformations ensure that the final image maintains spatial coherence and depth, providing a realistic representation of the 3D scene. Projection transforms the 3D scene into a 2D image, maintaining the perspective and depth cues. Clipping removes parts of objects that are outside the camera's view or obstructed by other objects, ensuring that only visible parts are rendered.

Dynamics and Physics: Simulating the Real World

Simulating real-world dynamics involves complex geometric computations to achieve believable animations.

• Collision detection & response: Collision detection algorithms use geometric properties to identify when objects intersect. By calculating collision points and response vectors, animators can simulate realistic impacts and interactions between objects. Bounding volumes, simple geometric shapes enclosing complex objects are used for initial collision checks, while more detailed algorithms handle precise interactions.

• Fluid dynamics and particle systems: Simulating fluids and particles requires understanding geometric flow patterns and particle interactions. Algorithms model the movement and behavior of fluids and particles, creating realistic simulations of water, smoke, fire, and other natural phenomena. The Navier-Stokes equations describe fluid motion, while particle systems use many small particles following simple rules to create complex effects, emulating Newton's laws.

• Kinematics & deformation: Kinematics and elasticity involve geometric transformations to simulate object movement and deformation. By applying principles of geometry, animators can create lifelike animations of objects bending, stretching, and returning to their original shapes. Inverse kinematics calculates joint movements to reach a desired position, while deformable models simulate how objects change shape under forces.

Conclusion

Geometric principles are integral to every stage of computer graphics, from the initial modeling to the final rendering. By mastering these principles, animators and graphic designers can create captivating and realistic digital worlds. For a deeper dive into how animators use math in their careers, check out the detailed article on the Business of animation website. For more on physically based rendering, refer to the comprehensive resource Physically based rendering: from theory to implementation.