Introduction

Skateboarding is a blend of art, skill, and physics. Each of these elements interplays seamlessly to create the fluid and captivating motion we see on ramps and skateparks. Skateboarders demonstrate an uncanny ability to maintain speed, even while navigating uphill sections of a park, and to build momentum without any external pushes. Their motion appears sleek and effortless, a testament to their mastery of technique and an underlying strategy known as pumping. Pumping is the key to understanding how skateboarders generate and sustain speed through precise shifts in body weight and movement. It combines intuition with principles of physics to achieve an elegant balance between effort and motion.

This blog will explore the pumping motion, delve into its mathematical modeling, and uncover why this strategy works so effectively to enhance performance.

Understanding the pumping motion

Imagine standing at the base of a mound on a skateboard park, ready to ascend without a single push off the ground. Skateboarders achieve this seemingly effortless feat through the pumping technique. This dynamic movement involves transferring energy to build and maintain momentum, even on upward slopes or curved transitions.

Step-by-step guide to pumping

• Step 1 - Standing position on the flat. The pumping action starts by standing in a relaxed, upright position while rolling along the flat bottom, maintaining balance and steady forward motion.

• Step 2 - Preparing for the curve. As one approaches the curve of the transition, one has to bend their knees and crouch slightly. This is more than just a squat; it involves thrusting your weight forward to set up for the upcoming motion.

• Step 3 - Entering the transition. In this phase, the skateboarder holds the crouched position as they move into the curve. The forward thrust aligns the body with the arc of the transition.

• Step 4 - The first pump. As one ascends the curve, they have to extend the legs and push their body upward. This motion is similar to swinging, which propells you higher into the transition.

• Step 5 - Reaching the apex. At the top of the transition, the skateboarder stops the thrust and transitions into a tucked position with the knees bent. This "reset" prepares the body for the downward motion.

• Step 6 - Descending the transition. On the way down, the knees are bent and the body is tucked to conserve momentum through the curve.

• Step 7 - The second pump. As one exits the transition onto the flat bottom, legs are straightened and weight is pushed downward. This generates additional speed for the next cycle.

• Step 8 - Reset and Repeat. The last stage is to return to the upright position and prepare to repeat the cycle. This continuous motion builds speed and control over ramps and transitions.

The information about the pumping process has been adapted from LearnToRideASkateboard.com, where you can find further resources and insights.

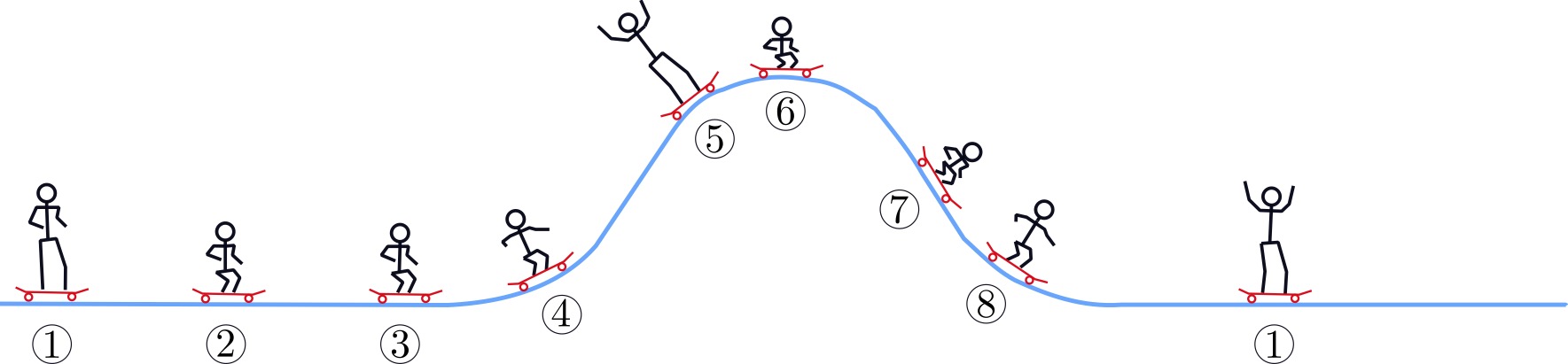Step by Step way to pump on a mound.

While these steps outline the process of pumping, the underlying physical principles are equally fascinating. The efficiency of pumping lies in its resemblance to a variable-length pendulum, with the skateboarder being the pendulum (we are head heavy and so an inverted pendulum). When ascending, extending the legs increases the pendulum's effective length (distance from wheels to the rider's center of mass), while crouching shortens it during descent. These timed adjustments inject energy into the system through parametric oscillations, much like pumping a swing. Mathematical modeling reveals how subtle shifts in body position translate to measurable speed gains, optimizing the skateboarder's path through transitions. By synchronizing with the ramp's curvature, riders harness kinetic and potential energy conversions, turning muscular effort into sustained momentum.

Mathematical modeling of pumping

To delve deeper into the mechanics of pumping, we model a skateboarder as a variable-length pendulum of length $L(t)$, adapting insights from the seminal paper "How to Pump a Swing?". Though a skateboarder can be modeled as an inverted pendulum, here we want to focus only on the mechanism of pumping. Thus we resort to the simpler swinging problem from hereon, however the broader qualitative takeaways are similar for skateboarding as well. The attached paper demonstrates how timed length variations of the pendulum, $\Delta L$ can amplify oscillations without external pushes, a similar principle skateboarders exploit through precise body movements. As shown in the figure below, the rider's crouching or standing changes the length $L$ corresponding to change in location of the center of mass $m$ from the pivot point $O$.

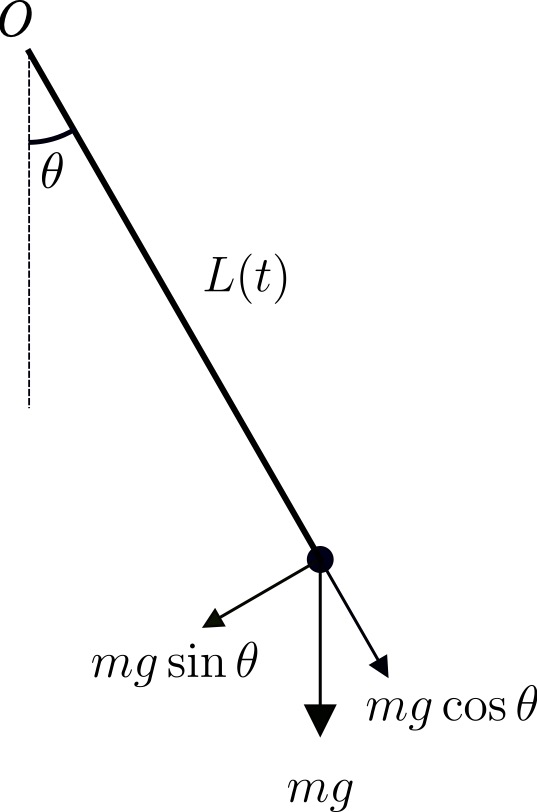
Schematic of a variable-length pendulum showing key forces acting on the mass. The pendulum has a length $L(t)$ varying as a function of time, an angular displacement $\theta(t)$, and experiences gravitational force $mg$. The force components are $mg \sin\theta$ (tangential) and $mg \cos\theta$ (radial).

A variable-length pendulum consists of the following components: the mass $m$ representing the skateboarder's body, the time-varying length $L(t)$, which is the distance from the pivot point to the center of mass, and the dynamic angular displacement $\theta(t)$, which measures the angle from the vertical. The angular momentum, $H(t)$ which quantifies rotational inertia, is given by $H(t) = mL^2(t)\dot{\theta}(t),$ where $\dot{\theta}(t)$ is the angular velocity (rate of rotation) and the torque, $N(t)$ which arises from gravity, is given by $N(t) = -mgL\sin\theta(t),$ here $g = 9.81 \, \text{m/s}^2$ is gravitational acceleration. By applying Newton's law $\dot{H}(t) = N(t)$, the equation of motion becomes, $\frac{d}{d t}\left( L^2(t) \dot{\theta}(t) \right) = -gL(t) \sin\theta(t).$

Skateboarders/Swing riders modulate the length of the pendulum $L$ strategically during a pumping cycle. Standing up ($L \downarrow$) occurs near $\theta \approx 0$ (the flat bottom of the ramp), while crouching ($L \uparrow$) occurs at $\theta_{\text{max}}$ (the apex of the ramp or swing). From angular momentum conservation, sudden changes in $L$ alter the angular velocity $\dot{\theta}$ as follows $\dot{\theta}^+ = \left( \frac{L_{\text{squat}}}{L_{\text{stand}}} \right)^2 \dot{\theta}^-,$ where $\dot{\theta}^-$ and $\dot{\theta}^+$ are angular velocities before and after standing up. For instance, if $L_{\text{squat}} = 1.5 \, \text{m}$ and $L_{\text{stand}} = 1.2 \, \text{m}$, then $\dot{\theta}^+ = \left( \frac{1.5}{1.2} \right)^2 \dot{\theta}^- \approx 1.56 \dot{\theta}^-.$ This represents a 56% increase in angular velocity. However, the tangential (linear) speed $v(t)$ is given by $v(t) = L(t) \, \dot{\theta}(t)$. In the crouched (squat) position, the speed is $v^- = L_{\text{squat}}\,\dot{\theta}^-,$ and after standing up it becomes, $v^+ = L_{\text{stand}}\,\dot{\theta}^+ = L_{\text{stand}} \left(\frac{L_{\text{squat}}}{L_{\text{stand}}}\right)^2 \dot{\theta}^- = \frac{L_{\text{squat}}^2}{L_{\text{stand}}}\,\dot{\theta}^-.$ Thus, the ratio of the speeds is, $\frac{v^+}{v^-} = \frac{L_{\text{squat}}^2/L_{\text{stand}}}{L_{\text{squat}}} = \frac{L_{\text{squat}}}{L_{\text{stand}}} = \frac{1.5}{1.2} = 1.25.$ This indicates a 25% increase in tangential speed.

So, if the skateboarder's tangential speed in the crouched phase is, for instance, 19.2 km/h, then after the pump cycle the speed becomes approximately $1.25 \times 19.2 \, \text{km/h} = 24.0 \, \text{km/h},$ yielding a net speed gain of about 4.8 km/h per pump cycle.
During the standing phase ($t_0 \leq t \leq t_0 + \Delta t$), with $|\theta| < \epsilon$, integration of the equation of motion reveals, $L_{\text{stand}}^2 \dot{\theta}_{\text{stand}} - L_{\text{squat}}^2 \dot{\theta}_{\text{squat}} = \int_{t_0}^{t_0 + \Delta t} \underbrace{gL \sin\theta}_{\approx 0} \, dt,$ which simplifies to: $L_{\text{stand}}^2 \dot{\theta}_{\text{stand}} = L_{\text{squat}}^2 \dot{\theta}_{\text{squat}}$. This negligible integral confirms that energy injection primarily occurs through changes in $L$, rather than through gravity.

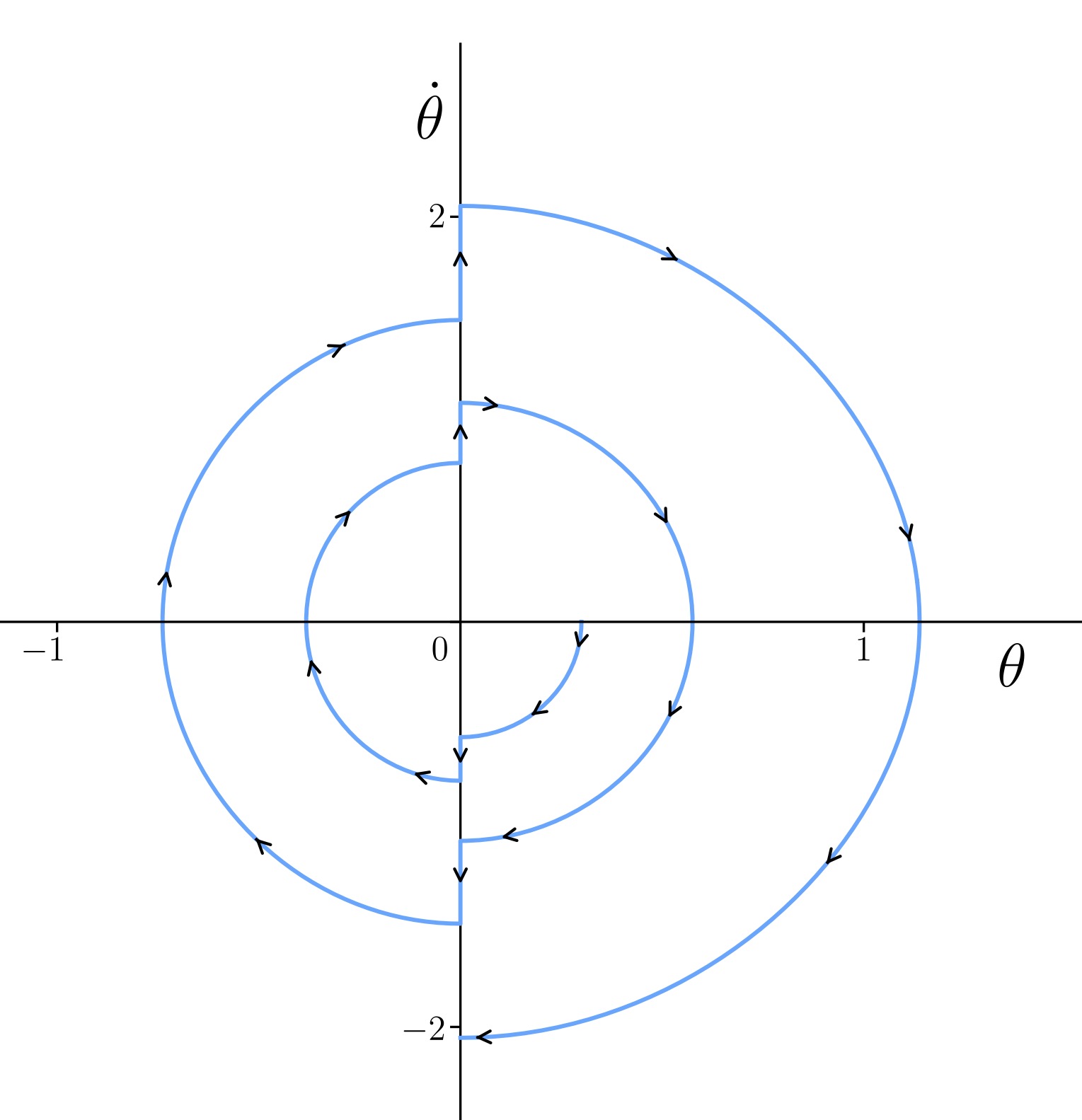
Phase portrait ($\theta(t)$ vs. $\dot{\theta}(t)$) of a variable-length pendulum illustrating energy accumulation through controlled length modulation. The simulation starts with an initial displacement $\theta_0 = 0.30$ rad and zero initial velocity ($\dot{\theta}_0 = 0$), using gravitational acceleration $g = 9.8$ m/s$^2$ and pendulum lengths $L_{\text{squat}} = 2.7$ m and $L_{\text{stand}} = 2.3$ m. Energy is injected at $\theta = 0$ (flat-bottom position) where the length instantaneously shortens, increasing angular velocity based on the scaling factor $(L_{\text{squat}} / L_{\text{stand}})^2$. The red arrows indicate the direction of motion in phase space, showing the system's evolution with each pumping cycle. The staircase-like jumps in $\dot{\theta}(t)$ correspond to discrete boosts in energy as the rider transitions from squatting to standing. The trajectory is generated using Python's solve_ivp function, with event handling for zero crossings and turning points. The integration alternates between squatting and standing phases, applying angular velocity boosts at transition points (at $\theta$ = 0).

Over successive cycles, the energy in the system accumulates with a net energy gain expressed as: $\Delta E = \frac{1}{2}m\left(L_{\text{squat}}^2\dot{\theta}_{\text{squat}}^2 - L_{\text{stand}}^2\dot{\theta}_{\text{stand}}^2\right) \approx \frac{1}{2}mv^2\left(\left(\frac{L_{\text{squat}}}{L_{\text{stand}}}\right)^2 - 1\right).$ This accumulated energy offsets friction and air resistance, enabling sustained or increased speed mimicking the way children pump swings to greater heights.

Conclusion

The pumping strategy in skateboarding is not just a clever trick--it reflects a simple strategy for actuation grounded in physics. By dynamically adjusting their stance to inject energy at the right moments, skateboarders employ a technique similar to bang-bang control. In simple terms, a bang-bang control is a simple strategy to make a system approach a desired state by driving the system with a forcing that switches abruptly between two extreme states, rather than making gradual adjustments. For further insights, check out my colleague Vishnu's post on bang-bang control, which offers a broader perspective on how this principle manifests across engineering and physics.

This article was inspired by two cool articles, the first being "Optimal strategies for Kiiking: active pumping to invert a swing", which explores how athletes use precisely timed squatting and standing cycles to inject energy into the system, a mechanism remarkably similar to the pumping motion of skateboarders. The other study was "Mechanical optimization of skateboard pumping", which presents a detailed mathematical model validating that skilled skateboarders naturally follow an optimal strategy by dynamically shifting their center of mass. These studies reinforce the idea that energy-efficient motion is not just a theoretical concept but is actively realized in human movement across different sports.